โมเมนตัม
โมเมนตัม

การคงตัวของโมเมนตัม
1. ก่อนการใช้กฎการคงตัวของโมเมนตัมกับปัญหาใด ขั้นแรกคุณต้องตัดสินว่าโมเมนตัมมีค่าคงตัวหรือไม่
โมเมนตัมมีค่าคงตัวถ้าผลบวกเวกเตอร์ของแรงภายนอกที่กระทำต่อระบบอนุภาคมีค่าเป็นศูนย์เท่านั้น
ถ้าเงื่อนไขนี้ไม่เป็นจริง คุณไม่สามารถใช้กฎการลงตัวของโมเมนตัมได้
2. นิยามระบบพิกัด วาดรูปแสดงแกนพิกัดทั้งทิศบวกสำหรับแต่ละแกน บ่อยครั้งวิธีง่ายที่สุดคือเลือกแกน
x ให้อยู่ในทิศของความเร็วหนึ่งให้แน่ใจว่าคุณกำลังใช้กรอบอ้างอิงเฉื่อยปัญหาส่วนใหญ่ในบทนี้เป็นปัญหาในสองมิติที่เวกเตอร์มีองค์ประกอบตามแกน
x และแกน y เท่านั้น ข้อความที่ตามมาต่อไปน้ามารถขยายให้รวมองค์ประกอบตามแกน
z ได้เมื่อจำเป็น
3. พิจารณาแต่ละวัตถุเป็นอนุภาค เขียนรูปสถานการณ์ ก่อนและ หลังและรวมทั้งใส่เวกเตอร์บนแต่ละรูปเพื่อแทนความเร็วที่รู้ค่าทั้งหมด
เขียนแสดงเวกเตอร์ด้วยขนาด มุม องค์ประกอบ หรือข้อมูลใดก็ตามที่กำหนดมาให้และกำหนดสัญลักษณ์พีชคณิตให้กับขนาด
มุม องค์ประกอบหรือข้อมูลใดก็ตามที่กำหนดมาให้ และกำหนดสัญลักษณ์พีชคณิตให้กับขนาด
มุม องค์ประกอบแต่ละปริมาณที่ไม่รู้ค่า คุณอาจพบว่าการใช้ตัวห้อย 1 และ 2 สำหรับความเร็วก่อนและหลังการกระทำระหว่งกันตามลำดับเป็นสิ่งที่มีประโยชน์
ถ้าคุณใช้ตัวห้อยเหล่านี้ก็ให้ใช้ตัวหนังสือเพื่อแทนแต่ละอนุภาค
4. เขียนสมการในรูปของสัญลักษณ์เทียบองค์ประกอบตามแกน x ตอนต้นทั้งหมด (นั่นคือก่อนการกระทำระหว่างกัน)
กับองค์ประกอบตามแกน x ตอนปลายทั้งหมด(นั่นคือหลังการกระทำระหว่างกัน)โดยใช้
px = mvx
สำหรับแต่ละอนุภาค เขียนสมการอีกสมการหนึ่งสำหรับอง๕ปนะกอบตามแกน yโดยใช้ py
= mvy สำหรับแต่ละอนุภาค จำไว้ว่าเราไม่มีวันเอาองค์ประกอบตามแกน xและตามแกน
yของความเร็วหรือโมเมนตัมมาบวกกันในสมการเดียวกัน แม้แต่เมื่อความเร็วทุกความเร็วอยู่ในแนวเส้นตรงเดียวกัน(เช่นแกน
x) องค์ประกอบของความเร็วตามเส้นนี้ก็สามารถเป็นบวกหรือลบได้ ให้ระวังเรื่องเครื่องหมาย!
5. แก้สมการเหล่านี้เพื่อหาผลอะไรก็ตามที่ต้องการ ในปัญหาบางข้อคุณจะต้องแปลงจากองค์ประกอบตามแกน
xและตามแกน y ของความเร็วไปเป็นขนาดและทิศของความเร็วหรือว่ากลับกัน
6. ในปัญหาบางข้อการพิจารณาเกี่ยวกับพลังงานจะให้ความสัมพันธ์ระหว่างความเร็วต่างๆเพิ่มเติม
ซึ่งเราจะเห็นต่อไปภายหลัง
สรุป
1. เรานิยามโมเมนตัม ![]() ของอนุภาค
m ซึ่งเคลื่อนที่ด้วยความเร็ว
ของอนุภาค
m ซึ่งเคลื่อนที่ด้วยความเร็ว ![]() ว่าคือปริมาณเวกเตอร์
ว่าคือปริมาณเวกเตอร์
![]()
ในรูปของโมเมนตัม เราสามารถเขียนกฎข้อที่ 2ของนิวตันสำหรับอนุภาคเป็น
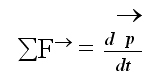
2. การดล ![]() ของแรงสุทธิคงตัว
ของแรงสุทธิคงตัว![]() ที่ทำในช่วงเวลาจากt1 ถึง t2 คือปริมาณเวกเตอร์
ที่ทำในช่วงเวลาจากt1 ถึง t2 คือปริมาณเวกเตอร์
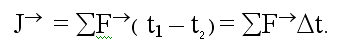
ถ้าแรงสุทธิแปรตามเวลาการดลคือ
![]()
การเปลี่ยนโมเมนตัมของอนุภาคในช่วงเวลาใดๆมีค่าเท่ากับการดลของแรงสุทธิที่ทำต่ออนุภาคในระหว่างช่วงเวลานั้น:
![]()
โมเมนตัมของอนุภาคมีค่าเท่ากับการดลที่เร่งอนุภาคนั้นจากหยุดนิ่งให้มีอัตราเร็วปัจจุบัน
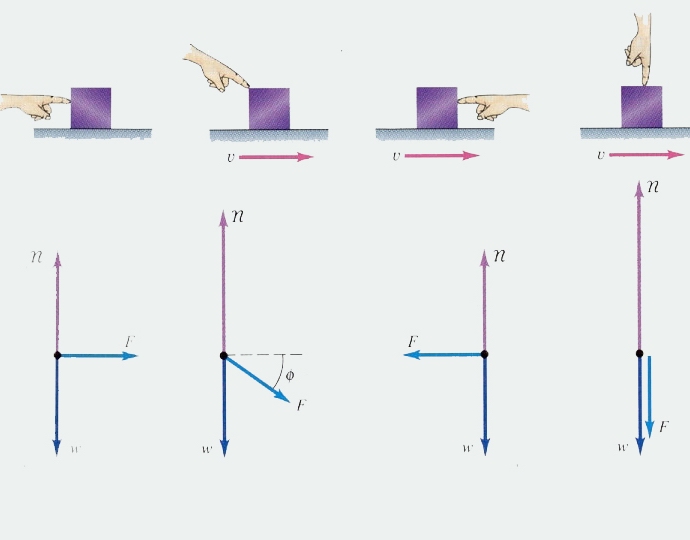
3. แรงภายในคือแรงที่ส่วนหนึ่งของระบบ ทำต่อส่วนอื่น แรงภายนอกคือแรงที่ของบางอย่างนอกระบบทำต่อส่วนหนึ่งของระบบ ระบบโดดเดี่ยวคือระบบที่ไม่มีแรงภายนอกใดทำ
4. โมเมนตัมทั้งหมดของระบบอนุภาค A,B,C คือผลบวกเวกเตอร์ของโมเมนตัมแต่ละอนุภาค:
![]()
ถ้าแรงภายนอกสุทธิที่ทำต่อระบบมีค่าเป็น 0 โมเมนตัมทั้งหมดของระบบมีค่าคงตัว แต่ละองค์ประกอบของโมเมนตัมทั้งหมดแยกกันมีค่าคงตัว
5. เราอาจแบ่งการชนตามความสัมพันธ์เชิงพลังงานและความเร็วสุดท้าย ในการชนแบบยืดหยุ่นระหว่างวัตถุสองชิ้น พลังงานจลน์ทั้งหมดตอนตั้งต้นและตอนสุดท้ายมีค่าเท่ากันและความเร็วสัมพัทธ์ก่อนและหลังการชนมีขนาดเท่ากัน ในการชนแบบไม่ยืดหยุ่นระหว่างวัตถุสองชิ้น พลังงานจลน์ตอนตั้งต้น ถ้าวัตถุทั้งสองมีความเร็วสุดท้ายเท่ากัน การชนนั้นเป็นกันชนไม่ยืดหยุ่นอย่างสมบูรณ์
7. พิกัด xcm และ ycm ของจุดศูนย์กลางมวลของระบบอนุภาคมีนิยามว่า
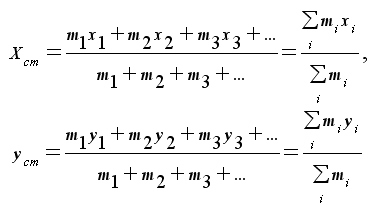
ในรูปของเวกเตอร์ตำแหน่ง 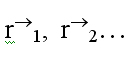 ของอนุภาคเวกเตอร์ตำแหน่ง
ของอนุภาคเวกเตอร์ตำแหน่ง![]() ของจุดศูนย์กลางมวลคือ
ของจุดศูนย์กลางมวลคือ
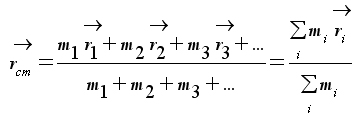
โมเมนตัมทั้งหมด ![]() ของระบบมีค่าเท่ากับมวลทั้งหมด
M ของระบบคูณกับความเร็ว
ของระบบมีค่าเท่ากับมวลทั้งหมด
M ของระบบคูณกับความเร็ว ![]() ของจุดศูนย์กลางมวลของระบบ:
ของจุดศูนย์กลางมวลของระบบ:
![]()
8. จุดศูนย์กลางของระบบเคลื่อนที่เหมือนกับมวลทั้งหมด M ไปรวมอยู่ที่จุดศูนย์กลางมวล
ถ้าแรงภายนอกสุทธิที่ทำต่อระบบเป็น 0 ความเร็วของจุดศูนย์กลางมวล![]() มีค่าคงตัว ถ้าแรงภายนอกสุทธิมีค่าไม่เป็น 0 จุดศูนย์กลางมวลจะมีความเร่ง:
มีค่าคงตัว ถ้าแรงภายนอกสุทธิมีค่าไม่เป็น 0 จุดศูนย์กลางมวลจะมีความเร่ง:
![]()